二阶魔方

二阶魔方（英语：Pocket Cube）又称口袋魔方、迷你魔方、小魔方、冰块魔方，为2×2×2的立方体结构。本身只有8个角块，没有其他结构的方块。结构与三阶魔方相近， 可以利用复原三阶魔方的公式进行复原。

发展历史

1974年，鲁比克教授发明了第一个魔方，即3×3×3立方体结构的“三阶魔方”（当时称作Magic Cube），并在1975年获得匈牙利专利号HU170062，但没有申请国际专利。第一批三阶魔方于1977年在布达佩斯的玩具店贩售。与Nichols的魔方不同，鲁比克教授的零件是像卡榫一般互相咬合在一起，不容易因为外力而分开，而且可以以任何材质制作。

1979年九月，Ideal Toys公司将魔方带至全世界，并于1980年一、二月在伦敦、巴黎和美国的国际玩具博览会亮相。

展出之后，Ideal Toys公司将魔方的名称改为Rubik's Cube，1980年五月，第一批魔方在匈牙利出口。

魔方广为大众喜爱是在1980年代。从1980年到1982年，总共售出了将近200万个魔方。据估计，1980年代中期，全世界有五分之一的人在玩魔方。

由于魔方的巨大商机，1983年鲁比克教授和他的合伙人一同开发了二阶和四阶魔方。并于1986年制造了五阶魔方。

8个角块的位置均可进行任意互换（8!种状态），如果以一个角块不动作为参考角块，其他7个角块都能任意转换方向（即37种状态）(注：这里指的转换方向，或者说翻转，是指一个角块从例如白-红-绿变成绿-白-红但是一次翻转一定会翻转到3个角块)。如果在空间中旋转则不计算方向不同而状态相同的魔方，实际上的准确状态数还应除以8。所以二阶魔方的总状态数为：

二阶魔方的最远复原距离（即最需要最多步骤复原的状态）为11次全旋转，或者14次普通旋转，此结果可以用计算机使用暴力穷举算法计算出。

复原方法

二阶魔方只有8个角块，可以利用“三阶魔方层先法”的一部分原理进行还原。

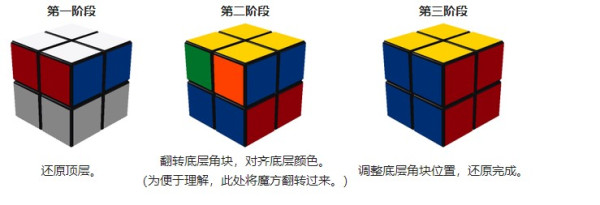
【参考来源：维基百科】